The Research Trimester (TR) of the CONTROL domain
A course dedicated to control theory
Control theory is a branch of applied mathematics that studies how to estimate, control and optimize the evolution of dynamic systems, i.e. systems whose state evolves over time under the effect of mathematical laws, such as the movement of planets, temperature variation or urban traffic management. This theory plays a central role in many scientific and industrial fields. Its objective is to guarantee that a system reaches a desired state and reacts robustly to disturbances and uncertainties. This discipline covers a wide range of issues, from the development of theoretical mathematical tools for different classes of dynamic systems (differential, partial differential, hybrid, delayed equations, etc.), under general assumptions of controllability, observability and regularity, up to the resolution of industrial problems applied to various fields such as mechanics, chemistry, electrical engineering, quantum physics, aeronautics, mechatronics, the automotive industry, the oil sector and energy. It also extends to disciplines related to applied mathematics, such as optimization, particularly through optimal control and estimation issues.
In this context, the CONTROL Research Term (TR) at Mines Paris – PSL offers second-year engineering students an immersion in this discipline through research projects carried out at the Centre Automatique et Systèmes (CAS) of Mines Paris – PSL or its partners. The aim is to provide them with the essential theoretical foundations, to enable them to apply the knowledge acquired in the first year and to introduce them to the advanced concepts that they will study in depth in the third year. This term also illustrates the scope of control theory in concrete applications, where the mastery of dynamic systems is a fundamental issue for innovation and technological competitiveness.
Spotlight on a 2025 student project
Understanding and improving a polynomial optimization method, or how to find the best choice without getting lost along the way
As part of the TR CONTROL, David Abulius, a 2nd year student in the Civil Engineering cycle, worked on a complex optimization subject aimed at improving a mathematical method used to find the global minimum of polynomial functions. More simply: how to find the best possible solution to a problem without getting trapped by less good intermediate solutions? This type of problem is fundamental in applied mathematics and is used in fields as varied as engineering, physics and artificial intelligence.
When trying to minimize a polynomial function in several variables, traditional methods often fail due to the presence of local minima. Imagine you are hiking in the mountains and looking for the lowest point in a valley. If you only look at what is right around you, you risk stopping in a local hollow without ever reaching the true lowest valley. This is exactly what happens when trying to minimize a mathematical function called a “polynomial”: traditional methods often fall into these “false minima”.
Jean-Bernard Lasserre, mathematician and Director of Research at the CNRS and Associate Member of the Toulouse School of Economics (TSE), has developed an approach that is widely used today and allows this global minimum to be approximated (and the lowest point of the valley to be approached), but which has certain limitations in terms of convergence and precision. The aim of David’s project was to study a new method proposed by his supervisor, Antoine Tilloy, a teacher-researcher at the CAS, which could be more effective but whose mathematical properties have yet to be demonstrated.
David Abulius explains:
“The optimization problem studied is that of the global minimization of a multivariate polynomial, without constraints, which is non-convex. The approach of Lasserre that we extend consists of limiting it by a succession of optimization problems of a linear function on a convex set. Unlike Lasserre, the constraint is not based on a priori (Lasserre’s method presupposes that we know in which surroundings a minimizer of the polynomial is found). The constraint of this new optimization problem is formulated as follows, where λ is the variable that approaches the minimum of p, G is a free variable that is a vector of polynomials, and σ is a polynomial written as a sum of squares:
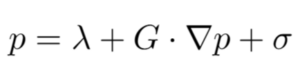
What is interesting about this formulation is that it involves the gradient of the polynomial (in other words, the measure of its variations). The gradient is local information, easy to obtain, and yet the optimization problem provides global information: the global minimum of the polynomial.
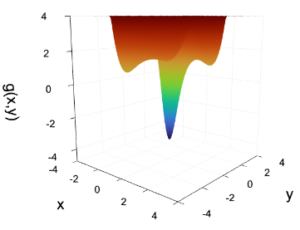
(Function graph of a polynomial of two variables with multiple minima)
As for the concrete applications of polynomial optimization methods, they are many and varied. For example, we have applications in the study of dynamic systems to find the associated Lyapunov function. The problem of optimal power flow, which consists of determining the best way to allocate energy production to generators while respecting the constraints of the electrical network, also makes extensive use of polynomial optimization.”
This project, which lies at the interface between optimization and algebraic geometry, has led David to explore in depth the theoretical foundations of existing methods, to implement algorithms and to empirically test the new approach. This work combines reading advanced articles, exploring conjectures and testing new mathematical concepts. The aim is to understand whether this approach could become a more effective tool for solving optimization problems in fields as varied as artificial intelligence, physics and engineering.
Past projects: a research internship serving the long term
The Trimestre Recherche (TR) internships are not only a scientific immersion for the students of Mines Paris – PSL: they are part of a long-term research dynamic for the laboratories that host them. By integrating ambitious projects, the engineering students make a concrete contribution that extends well beyond the few months of the internship. It is in this context that Maxence Lamarque, a student at Mines Paris – PSL, completed an internship in 2022 at the Centre Automatique et Systèmes (CAS) of Mines Paris – PSL, under the direction of Delphine Bresch-Pietri, teacher-researcher at CAS. His subject? An inverse Lyapunov theorem for delay equations and hyperbolic partial differential equations. In other words, Maxence focused on a mathematical theorem that characterizes a certain stability property for delay systems, i.e. systems where the dynamics and therefore the future evolution depend on both the current state and a past state. This property was that of Input-to-State Stability (ISS), a concept used to understand how a system reacts to external disturbances and to guarantee that, if the disturbance disappears, the system remains stable. Such a notion is essential to characterize the performance of a dynamic system with regard to uncontrolled inputs. For example, it can be used to quantify by how much a car will deviate from its nominal trajectory in the presence of a crosswind.
Understanding and controlling delay systems
During the TR CONTROL, Maxence Lamarque focused on delay systems, i.e. systems where the current evolution depends not only on their present state, but also on their past state. Imagine that you are driving a car with a reaction time of a few seconds: you only start to brake a little after you see an obstacle. This delay between the perception of danger and the action corresponds to a delay in the system. These delay systems are common in engineering, particularly in the case of signal transmission, due to calculation time or in the case of material flow.
The aim of Maxence’s project was to study how to guarantee the input-state stability of difference systems, a particular type of delay equation that is equivalent to hyperbolic partial differential equations. To do this, he used a mathematical tool called the Lyapunov functional, which quantifies the energy of the dynamic system in its current state. If this functional decreases over time in the absence of disturbance, and admits variations bounded by the amplitude of the disturbances, then the system is input-state stable. This property is well known for ordinary differential equations. Maxence’s work consisted in showing that this property is also true for difference equations. But he also proved the inverse property, known as the inverse Lyapunov property, that such a functional exists if the system is input-state stable.
It was the first time that I had worked in the field of control theory, and I particularly enjoyed tackling a technical and open subject, requiring me to overcome both computational and conceptual challenges. This attraction to the discipline was confirmed later during my gap year, when I did another research internship, and reinforced my desire to pursue a thesis after graduation.
Maxence Lamarque, P20 student
Major scientific and practical issues at stake
Why is the characterization of input-state stability interesting? Because having a Lyapunov function makes it possible to provide the input-state gain of the system, that is to say, the factor between the amplitude of the perturbations and that of the system response. If we take the example of a car subjected to a crosswind, this gain makes it possible to quantify the displacement of the car as a function of the intensity of the wind. We can then try to reduce this gain, for example with an adequate controller, i.e. a greater (delayed) reaction from the driver.
Similarly, in the field of health, some medical treatments use delayed control loops, such as smart insulin pumps for diabetics. Quantifying the impact of uncertainties is essential for the effectiveness of the treatment.
Thanks to his work, Maxence has contributed to the development of methodological tools for the analysis of the stability and robustness of these complex systems, thus paving the way for concrete applications in many technological fields.
Maxence had an excellent Research Quarter, enabling us to make significant progress on a difficult issue, despite limited time. His internship also opened up many perspectives, bringing real added value to this line of research.
Delphine Bresch-Pietri, teacher-researcher at the CAS, internship supervisor
A concrete and excellent experience
This internship perfectly illustrates the complementarity between theory and practice, which is at the heart of the pedagogy of Mines Paris – PSL. By carrying out real research work, the students of the Research Term make a tangible contribution to the laboratories that host them. For these structures, these internships are an opportunity to integrate motivated young talents, capable of bringing a fresh perspective and cutting-edge skills.
Maxime Lamarque’s work has resulted in an article, currently being proofread, in the journal Automatica. With his research on the understanding and control of delay systems, he is part of this dynamic: his internship was not limited to an academic exercise, but directly fed into cutting-edge research with tangible impact.
