Le Trimestre Recherche (TR) du domaine CONTROL
Un stage dédié à la théorie du contrôle
La théorie du contrôle est une branche des mathématiques appliquées qui étudie la façon d’estimer, de piloter et d’optimiser l’évolution des systèmes dynamiques, c’est-à-dire des systèmes dont l’état évolue au cours du temps sous l’effet de lois mathématiques, comme le mouvement des planètes, la variation de la température ou encore la gestion du trafic urbain. Cette théorie joue un rôle central dans de nombreux domaines scientifiques et industriels. Son objectif est de garantir qu’un système atteigne un état souhaité et réagisse de manière robuste aux perturbations et aux incertitudes. Cette discipline couvre un large éventail de problématiques, allant du développement d’outils mathématiques théoriques pour différentes classes de systèmes dynamiques (équations différentielles, aux dérivées partielles, hybrides, retardées, etc.), sous des hypothèses générales de commandabilité, d’observabilité et de régularité, jusqu’à la résolution de problèmes industriels appliqués à des domaines variés tels que la mécanique, la chimie, l’électrotechnique, la physique quantique, l’aéronautique, la mécatronique, l’automobile, le secteur pétrolier ou encore l’énergie. Elle s’étend également à des disciplines connexes des mathématiques appliquées, comme l’optimisation, en particulier à travers les questions de contrôle et d’estimation optimaux.
Dans ce contexte, le Trimestre Recherche (TR) CONTROL à Mines Paris – PSL offre aux élèves-ingénieurs de deuxième année une immersion dans cette discipline à travers des projets de recherche menés au sein du Centre Automatique et Systèmes (CAS) de Mines Paris – PSL ou de ses partenaires. L’objectif est de leur fournir les bases théoriques essentielles, de leur permettre d’appliquer les connaissances acquises en première année et de les initier aux concepts avancés qu’ils approfondiront en troisième année. Ce trimestre illustre également la portée de la théorie du contrôle dans des applications concrètes, où la maîtrise des systèmes dynamiques est un enjeu fondamental pour l’innovation et la compétitivité technologique.
Coup de projecteur sur un projet d’élèves 2025
Comprendre et améliorer une méthode d’optimisation polynomiale, ou comment trouver le meilleur choix sans se perdre en chemin
Dans le cadre du TR CONTROL, David Abulius, élève de 2e année du cycle Ingénieur Civil, a travaillé sur un sujet d’optimisation complexe visant à améliorer une méthode mathématique utilisée pour trouver le minimum global de fonctions polynomiales. Plus simplement : comment trouver la meilleure solution possible à un problème sans se laisser piéger par des solutions intermédiaires moins bonnes ? Ce type de problème est fondamental en mathématiques appliquées et intervient dans des domaines aussi variés que l’ingénierie, la physique et l’intelligence artificielle.
Lorsqu’on cherche à minimiser une fonction polynomiale en plusieurs variables, les méthodes classiques échouent souvent en raison de la présence de minima locaux. Imaginez que vous soyez en randonnée en montagne et que vous cherchiez le point le plus bas d’une vallée. Si vous ne regardez que ce qui est juste autour de vous, vous risquez de vous arrêter dans un creux local sans jamais atteindre la vraie vallée la plus basse. C’est exactement ce qui se passe lorsqu’on cherche à minimiser une fonction mathématique appelée « polynomiale » : les méthodes classiques tombent souvent dans ces « faux minima ».
Jean-Bernard Lasserre, mathématicien et Directeur de Recherche au CNRS et Membre Associé à la Toulouse School of Economics (TSE), a développé une approche largement utilisée aujourd’hui qui permet d’approximer ce minimum global (et d’approcher le point le plus bas de la vallée), mais qui présente certaines limites en termes de convergence et de précision. L’objectif du projet de David était d’étudier une nouvelle méthode proposée par son encadrant, Antoine Tilloy, enseignant-chercheur au CAS, qui pourrait être plus efficace mais dont les propriétés mathématiques restent encore à démontrer.
David Abulius explique :
« Le problème d’optimisation étudié est celui de la minimisation globale d’un polynôme multivarié, sans contraintes, qui est non convexe. L’approche de Lasserre que nous étendons, consiste à le borner par une succession de problèmes d’optimisation d’une fonction linéaire sur un ensemble convexe. À la différence de Lasserre, la contrainte ne repose pas sur des a priori (la méthode de Lasserre présuppose que l’on sache dans quels environs se trouve un minimiseur du polynôme). La contrainte de ce nouveau problème d’optimisation se formule comme suit, où λ est la variable qui approche le minimum de p, G est une variable libre qui est un vecteur de polynômes, et σ est un polynôme s’écrivant comme une somme de carré :
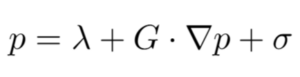
Ce qui est intéressant dans cette formulation, c’est qu’elle fait intervenir le gradient du polynôme (autrement dit la mesure de ses variations). Or le gradient est une information locale, facile à obtenir, et pourtant le problème d’optimisation donne une information globale : le minimum global du polynôme.
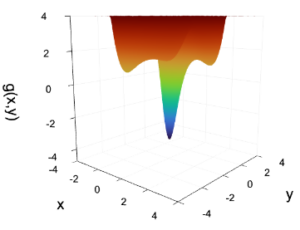
(Graphe de fonction d’un polynôme de deux variables avec multiples minimas)
Pour ce qui est des applications concrètes des méthodes d’optimisation polynomiale, elles sont nombreuses et diverses. Nous avons par exemple des applications dans l’étude de systèmes dynamiques pour trouver la fonction de Lyapunov associée. Le problème de l’optimal power flow, consistant à déterminer la meilleure façon d’allouer la production d’énergie aux générateurs tout en respectant les contraintes du réseau électrique, a lui aussi grandement recours à l’optimisation polynômiale.»
Ce projet, situé à l’interface entre optimisation et géométrie algébrique, a conduit David à explorer en profondeur les fondements théoriques des méthodes existantes, à implémenter des algorithmes et à tester empiriquement la nouvelle approche. Un travail mêlant lecture d’articles avancés, exploration de conjectures et mise à l’épreuve de nouveaux concepts mathématiques. L’intérêt étant de comprendre si cette approche pourrait devenir un outil plus performant pour résoudre des problèmes d’optimisation, dans des domaines aussi variés que l’intelligence artificielle, la physique ou l’ingénierie.
Les projets passés : un stage de recherche au service du temps long
Les stages de Trimestre Recherche (TR) ne sont pas seulement une immersion scientifique pour les élèves de Mines Paris – PSL : ils s’inscrivent dans une dynamique de recherche au long cours pour les laboratoires qui les accueillent. En intégrant des projets ambitieux, les élèves-ingénieurs apportent une contribution concrète qui se prolonge bien au-delà des quelques mois du stage. C’est dans ce cadre que Maxence Lamarque, étudiant à Mines Paris – PSL, a réalisé un stage en 2022 au sein du Centre Automatique et Systèmes (CAS) de Mines Paris – PSL, sous la direction de Delphine Bresch-Pietri, enseignante-chercheuse au CAS. Son sujet ? Un théorème de Lyapunov inverse pour équations à retard et équations aux dérivées partielles hyperboliques. Autrement dit, Maxence s’est intéressé à un théorème mathématique qui permet de caractériser une certaine propriété de stabilité pour des systèmes à retard, c’est-à-dire des systèmes où la dynamique et donc l’évolution future dépend à la fois de l’état actuel et d’un état passé. Cette propriété était celle de Stabilité Entrée-État (Input-to-State Stability, ISS), un concept utilisé pour comprendre comment un système réagit aux perturbations extérieures et garantir que, si la perturbation disparaît, le système reste stable. Une telle notion est essentielle pour caractériser les performances d’un système dynamique vis-à-vis d’entrées non maîtrisées. Par exemple, elle peut être utilisée pour quantifier de combien une voiture va s’éloigner de sa trajectoire nominale en présence de vent latéral.
Comprendre et maîtriser les systèmes à retard
Lors du TR CONTROL, Maxence Lamarque s’est intéressé aux systèmes à retard, c’est-à-dire des systèmes où l’évolution actuelle dépend non seulement de leur état présent, mais aussi de leur état passé. Imaginez que vous conduisiez une voiture avec un temps de réaction de quelques secondes : vous commencez à freiner seulement un peu après avoir vu un obstacle. Ce délai entre la perception du danger et l’action correspond à un retard dans le système. Ces systèmes à retard sont courants en ingénierie, notamment en cas de transmission de signaux, du fait de temps de calcul ou en cas de flux de matière.
L’objectif du projet de Maxence était d’étudier comment garantir la stabilité entrée-état de systèmes aux différences, un type particulier d’équations à retard qui sont équivalents à des équations aux dérivées partielles hyperboliques. Pour cela, il a utilisé un outil mathématique appelé fonctionnelle de Lyapunov, qui quantifie l’énergie du système dynamique dans son état actuel. Si cette fonctionnelle diminue au fil du temps en l’absence de perturbation, et admet des variations bornées par l’amplitude des perturbations, alors le système est stable entrée-état. Cette propriété est bien connue pour des équations différentielles ordinaires. Le travail de Maxence a consisté à montrer que cette propriété est également vraie pour les équations aux différences. Mais il a aussi prouvé la propriété inverse, dite de Lyapunov inverse, qu’une telle fonctionnelle existe si le système est stable entrée-état.
C’était la première fois que je travaillais dans le domaine de la théorie du contrôle, et j’ai particulièrement apprécié m’attaquer à un sujet technique et ouvert, nécessitant de surmonter des défis aussi bien calculatoires que conceptuels. Cet attrait pour la discipline s’est confirmé par la suite lors de ma césure, où j’ai poursuivi un autre stage de recherche, et a renforcé mon souhait de poursuivre en thèse après l’obtention de mon diplôme.
Maxence Lamarque, élève P20
Des enjeux scientifiques et pratiques majeurs
Pourquoi la caractérisation de la stabilité entrée-état est-elle intéressante ? Parce que disposer d’une fonction de Lyapunov permet de fournir le gain entrée-état du système, c’est-à-dire, le facteur entre l’amplitude des perturbations et celle de la réponse du système. Si l’on reprend l’exemple d’une voiture soumise à un vent latéral, ce gain permet de quantifier le déplacement de la voiture en fonction de l’intensité du vent. On peut alors chercher à diminuer ce gain, par exemple avec un contrôleur adéquat, c’est-à-dire une réaction (à retard) du conducteur plus importante.
De même, dans le domaine de la santé, certains traitements médicaux utilisent des boucles de régulation avec retard, comme les pompes à insuline intelligentes pour les diabétiques. Quantifier l’impact d’incertitudes est essentiel pour l’efficacité du traitement.
Grâce à son travail, Maxence a contribué au développement d’outils méthodologiques pour l’analyse de la stabilité et de la robustesse de ces systèmes complexes, ouvrant ainsi la voie à des applications concrètes dans de nombreux domaines technologiques.
Maxence a réalisé un excellent Trimestre Recherche, nous permettant de progresser significativement sur une question difficile, malgré un temps limité. Son stage a également ouvert de nombreuses perspectives, apportant une réelle valeur ajoutée à cet axe de recherche.
Delphine Bresch-Pietri, enseignante-chercheuse au CAS, encadrante du stage
Une expérience concrète et d’excellence
Ce stage illustre parfaitement la complémentarité entre théorie et pratique, au cœur de la pédagogie de Mines Paris – PSL. En réalisant un véritable travail de recherche, les étudiants du Trimestre Recherche apportent une contribution tangible aux laboratoires qui les accueillent. Pour ces structures, ces stages sont une opportunité d’intégrer des jeunes talents motivés, capables d’apporter un regard neuf et des compétences pointues.
Le travail de Maxime Lamarque a abouti à la rédaction d’un article, actuellement en relecture, dans la revue Automatica. Avec ses recherches sur la compréhension et la maîtrise des systèmes à retard, il s’inscrit dans cette dynamique : son stage ne s’est pas limité à un exercice académique, mais a directement nourri une recherche pointue à l’impact tangible.
