Une IA contrainte et informée par les mathématiques non-linéaires
Les recherches menées au CMA s’inscrivent dans une conviction forte : l’IA ne peut se limiter à l’accumulation de données et de paramètres. Pour être fiable, interprétable et réellement utile, elle doit s’appuyer sur des modèles mathématiques explicites.
C’est dans cet esprit que s’inscrit l’une des chaires PR[AI]RIE-PSAI (PaRis Artificial Intelligence Research InstitutE – Paris School of IA) portée par Jesus G. Angulo au CMA. Créée en 2019 par notre Université PSL ainsi que le CNRS, l’Inria, l’Institut Pasteur, l’Université Paris Cité et un groupe de partenaires industriels, PR[AI]RIE est l’un des quatre instituts interdisciplinaires de recherche en IA mis en place dans le cadre de la stratégie nationale pour l’IA annoncée par le président de la République en 2018. PR[AI]RIE-PSAI a pour objectif de devenir un leader mondial dans la recherche et l’enseignement supérieur en IA, avec un impact réel sur l’économie et la société.
Au sein de la chaire PR[AI]RIE-PSAI de J. G. Angulo, la morphologie mathématique fournit un langage commun pour décrire des formes, des structures et des relations spatiales complexes. Elle permet de formaliser des notions telles que la géométrie des données, leur topologie ou leur variabilité, là où les approches purement statistiques atteignent leurs limites.
Le contexte et l’objectif de la chaire est de combiner la puissance des réseaux de neurones (convolutifs ou transformers) avec des méthodes mathématiques rigoureuses de traitement d’image/données. En travaillant sur un socle théorique non-linéaire commun issu de la morphologie mathématique, certains paradigmes sont intégrés dans les réseaux de neurones :
- L’analyse topologique de données : elle consiste à étudier la forme globale des données (leurs regroupements, leurs trous, leurs connexions) plutôt que leurs valeurs précises, afin de repérer des structures cachées que les méthodes classiques ne voient pas.
- La géométrie stochastique : c’est une façon de décrire des données ou des phénomènes en tenant compte à la fois de leur géométrie (leur forme) et du hasard, par exemple pour modéliser des images bruitées ou des mesures incertaines.
- La géométrie tropicale : il s’agit d’une géométrie fondée sur des règles de calcul simplifiées (basées sur des maximums et des minimums) qui permet de représenter et d’analyser des formes complexes de manière plus stable et plus rapide pour les algorithmes.
- L’algèbre et théorie de représentation d’opérateurs : ces outils servent à décrire mathématiquement les transformations appliquées aux données (par exemple filtrer une image ou extraire une caractéristique) afin de mieux comprendre et contrôler le fonctionnement interne des réseaux de neurones.
- Les semi-groupes et les équations aux dérivées partielles (EDP) : ils permettent de modéliser l’évolution progressive d’un phénomène (comme la diffusion de la chaleur ou le lissage d’une image) et sont utilisés pour relier les réseaux de neurones à des lois physiques ou à des processus continus bien compris.
Hybridation des modèles
L’IA dialogue avec la physique et les contraintes réelles
Un autre axe majeur au CMA concerne l’hybridation entre apprentissage automatique, ou machine learning, et optimisation mathématique. Ces recherches, portées notamment par Sophie Demassey, trouvent leur application dans de nombreux systèmes industriels : réseaux d’eau potable, gestion de l’énergie, stockage… Dans ces domaines, les décisions doivent respecter des contraintes strictes : capacités physiques, règles de sécurité ou encore coûts énergétiques. Or, si les modèles d’apprentissage profond, ou deep learning, sont efficaces pour prédire des comportements à partir de données historiques, ils ne garantissent ni la faisabilité ni l’optimalité des décisions proposées.
La solution développée au CMA consiste à faire dialoguer prédiction et optimisation. Dans le cas de la gestion énergétique de réseaux d’eau, un réseau de neurones apprend à prédire des profils de stockage plausibles à partir des données passées. Ces prédictions servent ensuite de point de départ à un algorithme d’optimisation combinatoire, chargé de corriger et certifier la bonne solution.
- Résultat : des décisions rapides, économes en énergie, mais surtout mathématiquement garanties.
- Impact concret : une meilleure maîtrise des systèmes critiques, avec des gains énergétiques mesurables et une explicabilité accrue des choix opérés.
Résumer, comparer et apprendre à partir de distributions complexes
Un autre défi central de l’IA moderne est la gestion de données complexes telles que les images, les nuages de points ou encore les distributions de probabilités. Welington de Oliveira travaille sur une notion clé pour ces problématiques : le transport optimal. Chaque donnée est comme une pile de sable. Au lieu de comparer simplement deux piles, le transport optimal mesure l’effort minimal nécessaire pour transformer une pile en une autre, comme si on déplaçait le sable de manière optimale.
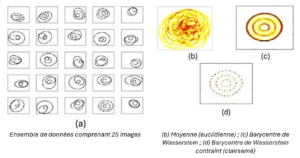
Pour quantifier cet effort, on utilise la distance de Wasserstein, qui évalue à quel point deux ensembles de données sont proches ou éloignés, même s’ils sont très complexes. Si vous avez plusieurs photos de chats, le transport optimal permet de calculer une image moyenne qui représente au mieux l’ensemble de ces photos. Cette image moyenne, appelée barycentre de Wasserstein, est une sorte de « portrait-robot » des chats photographiés.
Grâce aux travaux du CMA, il est désormais possible d’intégrer des règles supplémentaires lors du calcul de cette moyenne. Par exemple, on peut imposer de ne garder que les informations les plus importantes (sparsité), ou encore forcer le résultat à respecter une certaine structure pour qu’il reste réaliste. Grâce à des méthodes d’optimisation performantes, ces calculs deviennent possibles même pour des ensembles de données très volumineux.
Ces avancées permettent de développer des algorithmes plus robustes, capables de synthétiser et d’analyser des données complexes avec une grande précision. Les applications sont nombreuses : amélioration du traitement d’images, classification automatique d’objets, ou encore analyse de données rares ou incomplètes, comme des images médicales ou des relevés scientifiques. En somme, ces travaux aident l’IA à mieux appréhender la complexité du monde réel, pour des résultats plus fiables et utiles dans notre quotidien.
Mesurer la dissimilarité autrement en apprenant avec peu de données
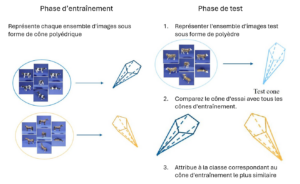
Dans certains domaines comme l’étude des maladies rares, la reconnaissance d’objets uniques ou l’écologie, les données disponibles sont souvent très limitées. Or, les méthodes traditionnelles d’IA peinent à fonctionner efficacement dans ces conditions, où l’on parle de Few-Shot Learning, un domaine qui consiste à apprendre à partir de très peu d’exemples.
Valentina Sessa et ses collègues ont développé une approche originale pour surmonter ce problème. Au lieu de représenter des ensembles d’images comme des espaces linéaires classiques, ils les modélisent sous la forme de cônes convexes, des structures géométriques mieux adaptées pour capturer la diversité et les variations des données. Pour comparer ces ensembles, ils ont mis au point une nouvelle mesure de dissimilarité, basée sur les angles maximaux et minimaux entre ces cônes.
Cette mesure est liée à une distance mathématique appelée distance de Pompeiu-Hausdorff, qui permet d’évaluer plus finement les différences entre les groupes d’images. Cette méthode repose sur des algorithmes d’optimisation non convexes, conçus pour garantir des calculs fiables même dans des situations complexes. Grâce à cette innovation, il devient possible de mieux distinguer des catégories différentes même avec très peu d’exemples à disposition.
L’impact est significatif : cette approche améliore les performances de l’IA dans des contextes où les données sont rares, difficiles ou coûteuses à obtenir, comme le diagnostic de maladies peu fréquentes ou l’identification d’espèces animales à partir de quelques observations. Elle ouvre ainsi la voie à des applications plus précises et plus robustes, même lorsque les informations disponibles sont limitées.
Le Workshop AI pour faire dialoguer un écosystème de recherche
Ces travaux ont été mis en lumière lors du Workshop IA organisé en décembre 2025 à Mines Paris – PSL. Pensé comme un moment d’échange interne, l’événement a permis aux enseignants-chercheurs, doctorants et ingénieurs de présenter leurs projets, outils et plateformes, à travers des présentations orales et des posters.
Au-delà de la diversité des sujets, le workshop a souligné une dynamique commune : construire une IA ancrée dans le réel, capable de dialoguer avec les humains et de s’intégrer dans des systèmes complexes.
Vers une IA plus sobre, plus explicable et plus responsable
Au-delà des résultats techniques, les recherches en IA du CMA partagent une ambition commune : développer une intelligence artificielle plus raisonnable, au sens du rapport entre moyens et besoins.
Face à la course aux modèles toujours plus volumineux et énergivores, les mathématiques offrent une alternative :
- Moins de données
- Moins de calcul
- Plus d’interprétabilité
- Meilleure intégration des lois physiques et des contraintes environnementales
Cette approche s’inscrit pleinement dans une démarche de sobriété numérique et de conception responsable, en phase avec les enjeux de transition écologique et industrielle.
Au CMA, l’IA n’est pas seulement une technologie : c’est un objet scientifique à part entière. En l’ancrant dans des cadres mathématiques solides, les chercheurs du centre contribuent à dessiner une IA plus fiable, plus compréhensible et plus durable, une IA pensée pour répondre aux défis réels de notre société.
Pour aller plus loin
- Valentin Penaud–Polge, Santiago Velasco-Forero, Jesus Angulo. Group Equivariant Morphological Networks. SIAM Journal on Imaging Sciences, 2025, 18 (4), pp.2236-2276. ⟨10.1137/24M1685766⟩. ⟨hal-05422798⟩
- Angulo, G.J. (2026). A Mathematical Morphology View of the Universal Representation of Scattering Networks. In: Wilkinson, M.H.F., Kosinka, J. (eds) Discrete Geometry and Mathematical Morphology. DGMM 2025. Lecture Notes in Computer Science, vol 16296. Springer, Cham.
- Jesus Angulo. Group Morphology Fixed Points on Homogenous Spaces for Deep Learning Equivariant Networks. GSI 2025, Oct 2025, Saint Malo (FR), France. ⟨hal-05319499⟩ Mimouni, P Malisani, J. Zhu, W. de Oliveira. Computing Wasserstein Barycenter via operator splitting: the method of averaged marginals. 2023. ⟨hal-04160009v4⟩
- Daniel Mimouni, Welington de Oliveira, Gregorio M Sempere. On the Computation of Constrained Wasserstein Barycenters. 2025. ⟨hal-05216990⟩ de Oliveira, V. Sessa, D. Sossa. Measuring dissimilarity between convex cones by means of max-min angles. ArXiv, 2025.
